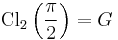Clausen function
In mathematics, the Clausen function is defined by the following integral:
It was introduced by Thomas Clausen (1832).
The Lobachevsky function Λ or Л is essentially the same function with a change of variable:
though the name "Lobachevsky function" is not quite historically accurate, as Lobachevsky's formulas for hyperbolic volume used the slightly different function
Contents |
General definition
More generally, one defines
which is valid for complex s with Re s >1. The definition may be extended to all of the complex plane through analytic continuation.
Relation to polylogarithm
It is related to the polylogarithm by
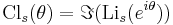 .
.
Kummer's relation
Ernst Kummer and Rogers give the relation
valid for 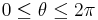 .
.
Relation to Dirichlet L-functions
For rational values of 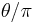 (that is, for
(that is, for  for some integers p and q), the function
for some integers p and q), the function 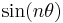 can be understood to represent a periodic orbit of an element in the cyclic group, and thus
can be understood to represent a periodic orbit of an element in the cyclic group, and thus 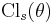 can be expressed as a simple sum involving the Hurwitz zeta function. This allows relations between certain Dirichlet L-functions to be easily computed.
can be expressed as a simple sum involving the Hurwitz zeta function. This allows relations between certain Dirichlet L-functions to be easily computed.
Series acceleration
A series acceleration for the Clausen function is given by
which holds for 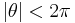 . Here,
. Here, 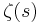 is the Riemann zeta function. A more rapidly convergent form is given by
is the Riemann zeta function. A more rapidly convergent form is given by
Convergence is aided by the fact that 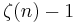 approaches zero rapidly for large values of n. Both forms are obtainable through the types of resummation techniques used to obtain rational zeta series. (ref. Borwein, etal. 2000, below).
approaches zero rapidly for large values of n. Both forms are obtainable through the types of resummation techniques used to obtain rational zeta series. (ref. Borwein, etal. 2000, below).
Special values
Some special values include
where G is Catalan's constant.
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 27.8", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 1005, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_1005.htm.
- Clausen, Thomas (1832). "Über die Function sin φ + (1/22) sin 2φ + (1/32) sin 3φ + etc.". Journal für die Reine und Angewandte Mathematik. [Crelle's Journal] 8: 298–300. ISSN 0075-4102. http://resolver.sub.uni-goettingen.de/purl?PPN243919689_0008
- Leonard Lewin, (Ed.). Structural Properties of Polylogarithms (1991) American Mathematical Society, Providence, RI. ISBN 0-8218-4532-2
- Jonathan M. Borwein, David M. Bradley, Richard E. Crandall (2000). "Computational Strategies for the Riemann Zeta Function". J. Comp. App. Math. 121: p.11. http://www.maths.ex.ac.uk/~mwatkins/zeta/borwein1.pdf.
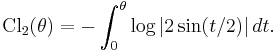
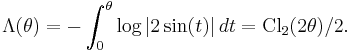
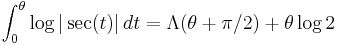
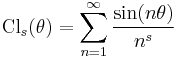
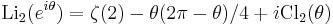
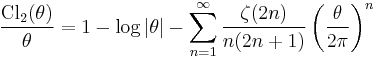
![\frac{\operatorname{Cl}_2(\theta)}{\theta} =
3-\log\left[|\theta| \left(1-\frac{\theta^2}{4\pi^2}\right)\right]
-\frac{2\pi}{\theta} \log \left( \frac{2\pi%2B\theta}{2\pi-\theta}\right)
%2B\sum_{n=1}^\infty \frac{\zeta(2n)-1}{n(2n%2B1)} \left(\frac{\theta}{2\pi}\right)^n](/2012-wikipedia_en_all_nopic_01_2012/I/f3f56ad7fa422c7160708151140956ec.png)